Any 'body' absorbs and emits radiation (a central heating 'radiator' does this - so do you. If we leave something in the sun it warms up as it absorbs infra-red radiation ...). As things get hotter they emit radiation at higher and higher frequencies - first at infra-red, then they may glow red, then orange ... white hot ... into the ultra-violet ... and os on. In fact they don't just emit with a single frequency but over a whole spectrum. Black Body radiation is radiation from a theoretical perfect emitter. This can be closely approximated by a cavity (box) with a very black lining and only a small hole were the escaping radiation can be observed.

There are 2 experimental 'laws' that describe the from of the radiation:

Wien's Displacement Law
$$ {\lambda_{max}} = {{2.898 \times 10^{-3}} \over {T}} $$
Which describes (at least at higher frequencies) the wavelength at which maximum radiation emission occurs at a temperature, T.

and Stefan's Law

$$ P = \sigma T^4 $$
Which describes the power output at a given temperature, T. (\(\sigma\) is the Stefan-Boltzman constant \(= 5.670373 \times 10^{-8} Wm^{-2}K{-4}\)


Classical physics analysed this by thinking about energy as waves within the box, bouncing around and exchanging energy with the walls of the cavity.

This was done by Lord Rayleigh and (independently) by Sir James Jeans to give the Rayleigh-Jeans Law. Unfortunately this doesn't actually match observations and, at short wavelengths, predicts infinite radiation intensity - Bugger!

All this was resolved in 1900 by a German physicist going by the rather wonderful name of Max Karl Ernst Ludwig Planck (let's have no more jokes about being as thick as a plank please!) - actually, Einstein had a lot to do with it too!

Building on the ideas of Boltzman's statistical approach to thermodynamics, Planck postulated that energy could only be emitted or observed in distinct, discrete 'quantised' packets (see where this is going yet?) described by the equation:
$$ E=h\nu$$
Where \(E\) is the energy, \(\nu\) is the frequency and \(h\) is Planck's constant (which very small: \(6.62607004 × 10^{-34} m^{2} kg s^{-1}\))

Apparently he really hated the idea - but it worked and he was awarded the 1918 Nobel prize for Physics - which can't be bad can it?

Newton had thought that light was composed of very small particles. However, experiments had tended to show that it was, in fact, a wave. Have a look at the 2-slit experiment to be convinced (light passing through 2 small slits produces an interference pattern on the other side - easily explained by classical wave-like theories).

However ... once again pesky experimental results didn't all work out like this. In the photoelectric effect, electrons can be 'knocked' off a surface by incident electromagnetic radiation (let's just call this 'light' for simplicity). Classical physics predicts that the energy of these freed electrons would increase with the INTENSITY of light. However, in 1902 experiments by Philipp Lenard showed that the energy of these liberated electrons actually increased with the FREQUENCY of the incident light. Once again - Bugger!

I suppose it was inevitable that Einstein would get in on the act somewhere - so it might as well be here.

Einstein explained the photoelectric effect by postulating that light actually existed as quanta of energy effectively described by the same principles that Planck had used to explain the blackbody radiation (see above).

He got his Nobel prize for this in 1921 - oddly not for his 'Relativity' theories for which he is best known.

This, of course opened up a whole bag of worms now referred to as the wave-particle duality (is it a wave? is it a particle? No! it's .... something else).

In the early years of the 20th century Ernest Rutherford (along with Hans Geiger and Ernest Marsden) whilst at Manchester University (my alma mater) did his seminal experiment probing the structure of the atom. He knew that an atom was composed of some positive and negative particles (known to be electrons) but not how they were arranged. They might be something like a plumb pudding with electrons embedded in a positive matrix. or there might be a central positive nucleus surrounded by electrons or ...

The experiment involved firing alpha particles (now known to be a Helium nucleus composed of 2 positive protons and 2 neutral neutrons) at a thin sheet of gold foil. The surprising result from this was that some (but not many) alpha particles were deflected through large angles back towards the source. This result has been described as as like an artillery shell being bounced back by a sheet of tissue paper.

The conclusion is that an atom must be composed of a very small, densely packed positively charged nucleus surrounded by a cloud of electrons. This, not surprisingly, is known as the Rutherford model of the atom.

We might now explain the atom as being a small positive nucleus with atoms 'orbiting;' around it just like our Solar System. This is an attractive model but classical physics predicts (and experiment shows) that an accelerating charge will emit and therefore lose energy. An orbiting electron is accelerating (it has to be as it is changing it's direction constantly as it moves in a circle). So, as it loses energy it must 'fall' towards the nucleus - in other words this model is unstable and can't be correct.

Bugger, Bugger - not again!

Neils Bohr, who had also worked at Manchester, proposed a modified model. In this model electrons orbited the electron in fixed energy orbits only - and couldn't orbit between these. The electron could change orbit by emitting a fixed amount of quantised energy (thanks Planck) equal to the difference in energy between the two orbits.

This was nice because it also explained observations of the visible emission spectra of exited hydrogen atoms such as the 'Balmer series' which had been described in the 1880's.

There's something vaguely unsatisfactory about just assuming that electrons can only exist in discrete orbits - why?

So let's come to de Broglie. He postulated that if something thought of as a wave - light - can be considered as a particle, why can't particles be considered as waves? Actually I'm sure his thought processes were bit more complex but bear with me, you never know it might be fun!

If you remember, Planck's quanta of energy (later confirmed by and extended to the concept of light 'photons' by Einstein) have energy \(E = h \nu \) and momentum, \({p}={h \over \lambda}\).

So now, if we consider something like an electron which possesses momentum, we can assign it a 'wavelength' $$ {\lambda} = {h \over p}$$ TaDaaaa!

You may say something like "What rot - that means a snooker ball must have a wavelength - but I don't see much evidence of wave-like interference effects between snooker balls!". Good point but hang on a minute, consider the numbers!

An electron has a mass of \(9.1\times10^{-31} kg\) and a typical velocity of, say, \(6\times10^6 m/s\) giving a wavelength of \(1.2\times10{-10} m\) - which is of the order of the diameter of an atom so we might expect to observe electron interference there. But similar properties of snooker balls (m=0.16 kg, v=4 m/s) give a wavelength of around \(10^{-34} m\) - which is pretty bloody small and unlikely to be noticeable in the 'real' world!

So how does this help? Well in a hand waving sort of way, you can see that a particle in an orbit in an atom can only exist as a sort of standing wave that 'fits' a whole number of wavelengths - and so and orbiting electron can only exist with discrete wavelengths that fit 1,2,3,...n times into the orbit. Neat ehh?

(You can also use this to work out the simple energy levels of an hydrogen atom by considering that the electron must fit in a parallel sided 'energy well' or box. If we consider the 'box' to have a length 'L' then the electron 'wave' must be a standing wave of wavelength 2L, 2L/2, 2L/3 ... 2L/n (nodes at the sides of the box). With a bit of jiggerey-pokerey you can actually get some quite nice agreement with observations).

The first experimental confirmation of de Broglie's ideas came from work done by Davisson and Germer in the middle of the 1920s.

They noted that electrons fired at crystalline nickel surface produced 'reflective' diffraction patterns analogous to X-ray patterns caused by the regular lattice structures in the crystals given by Bragg's Law:

$$ {n\lambda} = {2d sin \left( 90^o - {{\theta} \over 2} \right) } $$

Where n=1,2,3 ... and d is the spacing of the crystal lattice.

B-G found an experimental first maxima (n=1) at \(50^o\) for a 'd' (found earlier by X-Ray diffraction) of 0.091 nm using an electron source giving electrons of energy 54 eV.

If you plug these values into the Bragg equation you get an equivalent wavelength of 0.165 nm - which matches very well the theoretical de Broglie wavelength for electrons of the same energy of 0.167 nm.

Some more hand-waving!

Let's accept that a particle can be a wave (gulp!). What does that mean? For a wave to have a single wavelength, it must exist over a large distance (if it didn't it would just be a 'blip' without a wavelength as such. But this means that our particle is smeared out over space too. How can we make it more localised and particle-like? Well if we add a number of waves together of carefully chosen wavelengths we can get a sort of interference pattern that looks a lot more compact. Noddy illustration follows: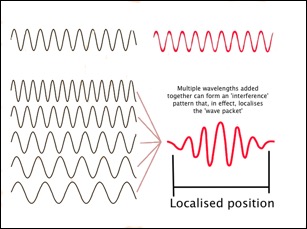

Well, good, that looks much better - but wait - unfortunately, this has consequences. If we have a nicely localised blip so that we can determine its position, then we can't know its wavelength - it's a mix. So, bearing in mind the de Broglie stuff (\( {p} = {h \over \lambda} \)), we can't know its momentum very well? Conversely, for the nice single wavelength, we know it's momentum really well - but not its position!

In essence this is the Heisenberg Uncertainty principle. Werner Heisenberg introduced his eponymous principle in 1927 and this states:

$$ {\sigma_x \sigma_p}={{h} \over {4\pi}} $$

Where \(\sigma_x\) is uncertainty of position and \(\sigma_p\) is uncertainty in momentum - and, by now, we all know what \(h\) is don't we? In other words, HOWEVER HARD WE TRY, we just CAN'T know, at the same time, both the position and momentum (and hence speed) of a particle. This is not about making better instruments, it is a fundamental restriction of nature.

This uncertainty actually applies to other special pairs of properties - for example Energy and Time.

A word of warning this is NOT the same as the idea that any observation of a particle will affect it in some way so that it's position/momentum is different after the observation - that's another story.

Finally, let's wrap this all up and put it to bed. We've seen that many things we thought were obvious are wrong - or rather, don't really conform to 'common sense' - and most particularly seen the 'wave-particle' duality conundrum.

In 1926 Erwin Shrödinger combined all this into a single differential equation - for which he was awarded the Nobel Prose in 1933.

The work we've seen earlier led to a central postulate in Quantum Mechanics that effectively states that all the measurable properties of a particle can be described by a complex valued 'wave function' (usually represented as \(\Psi\)). I'm not going to go into any more depth here - mostly because I don't think I really understand it!

Moving on - Shrödinger used this in a single formula (actually it can be written down in a number of ways depending on what question you're going to ask next). Here's the positional, time-dependent form for a non-relativistic particle:

$$ {i\hbar {{\partial} \over {\partial t}} \Psi (r, t)} = {\left[ {{-\hbar^2} \over {2\mu}}\nabla^2 + V(r, t) \right] \Psi(r, t)} $$

Look up what the symbols are if you're really interested but it included \(\mu\) the particles 'reduced mass' and \(V\) its potential energy, so effectively this states that the 'total energy' is equal to the 'kinetic energy' plus the 'potential energy' - so not as strange as you might think at first glance.

The interesting thing about \(\Psi\) is that if you 'square' it (actually it's complex so you multiply it by its complex conjugate) you get a formula that gives you the probability of finding the particle at any given point - a so called probability density function. So, in the absence of any observation, a particle could be anywhere - but is more likely to be in some positions than others. It's only when you go looking for it (make an observation) that the wave function 'collapses' and you can actually determine it's position. This is the Copenhagen interpretation of what the quantum world 'is'.

The whole idea about what constitutes an 'observation' is all a bit of a can of worms - which is where The Cat comes in. But first we need to sort out another difficult concept.

We've just mentioned 'position' so far but a particle has many parameters or properties encapsulated in its wavefunction(s) and they all are probabilistic in nature which means you don't know what they are until you look. But it's actually a bit more difficult than that. Until you look, the particle actually exists in all possible states at the same time - a state of affairs described as a superposition of states.

Back to the The Cat. The thought experiment describes a cat that is put into a box with a poison capsule that is triggered by a mechanism that depends on the decay of an atomic particle. Now this decay is a probabilistic quantum phenomenon so, until we look, we can't know if it has decayed yet. From the above stuff, this means that the particle is in a superposition of 2 states - decayed and un-decayed. Meaning that, until we look the particle has both triggered and not-triggered the poison - so is The Cat dead or not?

Usually this degenerates into a statement along the lines that The Cat is both dead and alive. But we know that in the 'real' world this is rubbish - a cat can't be both dead and alive. BUT, this now strikes at the concept of an observation. We can show experimentally that the idea of superposition at a particle level is a genuine phenomenon - but it obviously isn't at our large-scale, macro level of existence. So, what constitutes an observation, does it require an sentient being - or is it something to do with scale? This is still under debate. Have look at the 'Many Worlds' interpretation that essentially says that at every 'decision' point, the universe splits into 2 new realities - in this instance one where the cat is dead and one where it is alive.

Oh - if you're remotely interested the quote on the left is from the song 'White Rabbit' on the 'Surrealistic Pillow' album by Jefferson Airplane in 1967. All rather surreal - a bit like 'Alice's Adventures in Wonderland' really - and probably drug related in some way. Not unlike Quantum Mechanics I feel.